
Jedes Simulationsmodell hat Modellparameter.
Bei einer Modellsimulation muss man jedem Parameter einen konkreten Wert zuweisen.
Woher aber soll man wissen, welcher Wert für welchen Parameter am besten geeignet ist?
Eine Möglichkeit wäre, einfach jede Zahl, die einem zufällig in den Sinn kommt, auszuprobieren und nach Ablauf der Simulation zu schauen, ob sich das Simulationsergebniss verbessert hat (also z.B. ob die Simulationskurve besser zu experimentellen Daten passt).
Allerdings ist diese Methode bei komplexen Modellen mit vielen Parametern recht umständlich.
Geschickter ist es, automatische Verfahren einzusetzen. In diesem Artikel geht es um zwei der bekanntesten Verfahren: Evolutionsstrategien und Genetische Algorithmen.
Beide Methoden imitieren evolutionäre Prozesse, wie sie in der Biologie ablaufen.
Beispiel für ein Optimierungsproblem
Angenommen, wir haben folgendes Modell und wollen den höchsten Punkt finden:
Im Wertebereich von 0 < x < 10 und 0 < y < 10 ergibt sich foldende Landschaft:
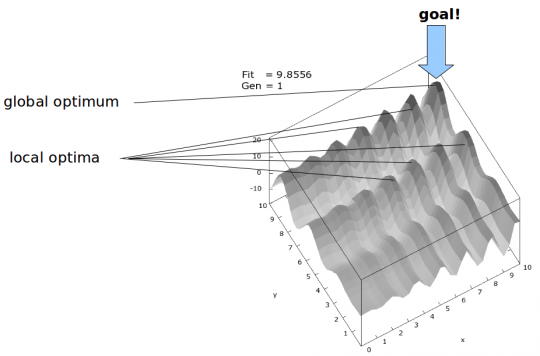
Den höchsten Gipfel (globales Optimum) zu finden, ist gar nicht so leicht.
Es gibt in dieser Landschaft viele kleinere Gipfel (lokale Optima). Das ist ein Problem, weil der Algorithmus nicht direkt unterscheiden kann, ob es sich bei einem bestimmten Gipfel um ein lokales oder das globale Optimum handelt.
Schauen wir nun, wie die beiden Optimierungsalgorithmen dabei helfen können, den höchsten Gipfel zu finden …
Lösung mit Evolutionsstrategie
Evolutionsstrategien imitieren die ungeschlechtliche Vermehrung: Ein einziges Individuum kann ohne fremde Hilfe Nachkommen erzeugen, die ihm genetisch sehr ähnlich sind. Durch kleinere Mutationen unterscheiden sich die Nachkommen jedoch geringfügig voneinander. Die Mutationen können neben den genetischen Eigenschaften (Genotyp), auch die äußeren Eigenschaften (Phänotyp) des Individuums verändern. So kann zum Beispiel ein leicht mutiertes Gänseblümchen intensiver duften als seine Geschwister und deshalb mehr Bienen anlocken – ein klarer Vorteil gegenüber der Konkurrenz. Das mutierte Gänseblümchen ist besser an seine Umwelt angepasst.
Dieses biologische Wissen können wir jetzt auf Simlationsmodelle übertragen.
Angenommen, wir wollen ein Modell mit vier Parametern optimieren (Aus didaktischen Gründen lässt es sich mit vier Parametern leichter erklären; wir kehren nachher zu unserem Modell mit zwei Parametern zurück).
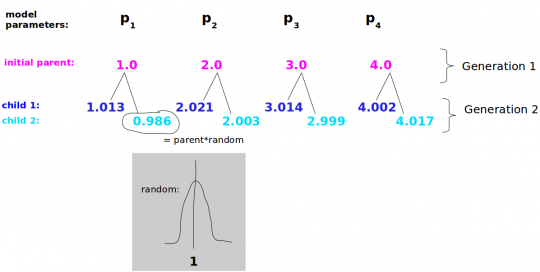
Zu Beginn gibt es einen einzigen Parametersatz, dem mehr oder weniger willkürliche Werte zugewiesen wurden (p1 = 1.0, p2 = 2.0 ….).

Die Nachkommen entstehen nun durch Multiplikation der Ausgangsparamter mit einer Zufallszahl.
Auf diese Weise entstehen zwei neue Parametersätze, „child 1“ und „child 2“.
Jetzt kann man für jeden dieser drei Parametersätze eine Modellsimulation durchführen und die sogenannte Modellfitness bestimmen (dazu später mehr).
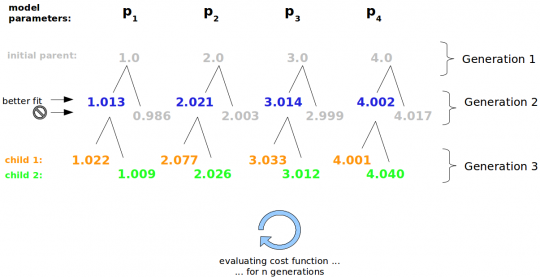
Nehmen wir an, der dukelblaue Parametersatz ist besser als die beiden anderen. Nun kann dieser Nachkommen hervorbringen, während die anderen beiden „Individuen“ vom Algorithmus nicht mehr beachtet werden. Anschließend wird für die neuen Parametersätze die Modellfitness bestimmt und wieder der Beste ausgewählt.
Dieser Prozess läuft so lange, bis ein guter Modellfit erreicht ist oder keine weitere Verbesserung der Modellfitness erfolgt.
Das folgende Video zeigt eine “live” Demonstration einer einfachen Evolutionsstrategie, die in unserer Modelllandschaft das globale Optimum (den höchsten Punkt) finden soll.
Zu Beginn setzen wir das erste Individuum mit drei Nachkommen an einem zufälligen Ort in dieser Landschaft aus.
Das beste Individuum ist durch einen roten Punkt dargestellt, alle anderen durch blaue Punkte – Ziel ist also, dass wenigstens der rote Punkt bis auf den höchsten Gipfel (rechts oben) klettert.
Drücke auf „play“, um das Video zu starten …
Schon nach wenigen Generationen hat die Evolutionsstrategie ein lokales Optimum gefunden, in dem sie jedoch stecken bleibt. Genau das ist ein typisches Problem einfacher Evolutionsstrategien – sie neigen in komplexen Landschaften dazu, an lokalen Optima hängen zu bleiben und nicht das globale Optimum zu finden. Zum Glück gibt es Methoden, mit denen man die lokalen Optima überwinden und den höchsten Gipfel erklimmen kann. Am bekanntesten ist der Genetische Algorithmus.
Lösung mit Genetischem Algorithmus
Genetische Algorithmen imitieren die geschlechtliche Fortpflanzung und das Verschmelzen von „mütterlichen“ und „väterlichen“ Chromosomen.
Der Algorithmus läuft folgendermaßen ab:
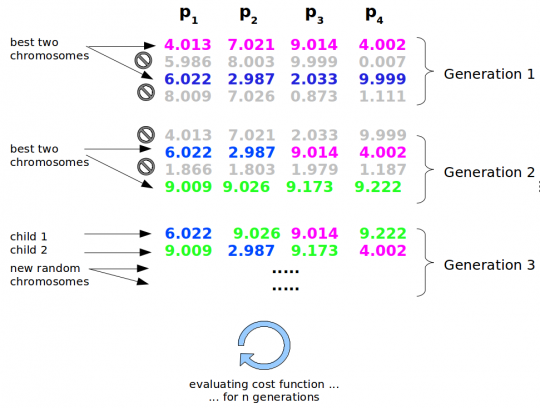
- Es entsteht eine vorher festgelegte Anzahl an Individuen. Die einzelnen Parameterwerte werden vollkommen zufällig festgelegt (allerdings innerhalb eines definierten Wertebereiches, hier von 0 bis 10).
- Anschließend wird für jedes Individium die Fitness bestimmt.
- Die „besten“ Individuen erzeugen Nachkommen, indem sie ihre genetischen Informationen kombinieren. Die beiden besten Parametersätze sind hier rosa und blau gefärbt. Das gemeinsame „Kind“ ist zur hälfte blau und zur hälfte rose
- Die übrigen Parametersätze werden einfach nicht mehr berücksichtigt und durch neue Parametersätze mit völlig zufälligen Werten ersetzt (grün).
- Dieser Prozess kann, je nach Komplexität des Modells, über mehrere hundert Generationen fortgesetzt werden.
Das folgende Video zeigt, wie der Genetische Algorithmus für unser Modell mit zwei Parametern das globale Optimum findet. Klicke auf „play“ und achte auf den roten Punkt im Video …
Zunächst werden den einzelnen Individuen zufällige Parameterwerte für x und y zugewiesen – deshalb sind die Punkte auch so verstreut. Im weiteren Verlauf entstehen neben den Nachkommen der besten Parameter auch immer wieder Parameter mit vollkommen zufälligen Werten. Deshalb „springen“ die Punkte so in der Landschaft umher.
Insgesamt ist der Genetische Algorithmus etwas langsamer als die Evolutionsstrategie, aber er findet das globale Optimum.
Anwendung
Wofür ist soll das Alles nun gut sein? Praktisch werden Genetische Algorithmen zum Beispiel angewendet, um komplexe dynamische Systeme wie Fahrpläne oder Stromnetze zu optimieren. Mir hat der Genetische Algorithmus bei meiner Dissertation und bei der Entwicklung eines Modells zur Epidemieausbreitung geholfen.